Traveltime calculation and raytracing

Calculate traveltimes in layered media

Here we will excercise two example how to calculate traveltimes for the phases P and Pg for different earth velocity models.

Modules covered in this example:

• pyrocko.cake

The first example is minimalistic and will give you a simple traveltime table.

Download cake_ray_tracing.py

'''
Calculate P-phase arrivals.
'''

from pyrocko import cake
import numpy as num

km = 1000.

# Load builtin 'prem-no-ocean' model (medium resolution)
model = cake.load_model('prem-no-ocean.m')

# Source depth [m].
source_depth = 300. * km

# Distances as a numpy array [deg].
distances = num.linspace(1500, 3000, 16)*km * cake.m2d

# Define the phase to use.
Phase = cake.PhaseDef('P')

# calculate distances and arrivals and print them:
print('distance [km]      time [s]')
for arrival in model.arrivals(distances, phases=Phase, zstart=source_depth):
    print('%13g %13g' % (arrival.x*cake.d2m/km, arrival.t))

The second code snippet includes some lines to plot a simple traveltime figure.

Download cake_ray_tracing.py

import numpy as num
from matplotlib import pyplot as plt

from pyrocko.plot import mpl_init, mpl_margins, mpl_papersize
from pyrocko import cake

fontsize = 9.
km = 1000.

mod = cake.load_model('ak135-f-continental.m')

phases = cake.PhaseDef.classic('Pg')
source_depth = 20.*km

distances = num.linspace(100.*km, 1000.*km, 100)

data = []
for distance in distances:
    rays = mod.arrivals(
        phases=phases, distances=[distance*cake.m2d], zstart=source_depth)
    for ray in rays[:1]:
        data.append((distance, ray.t))

phase_distances, phase_time = num.array(data, dtype=float).T

# Plot the arrival times
mpl_init(fontsize=fontsize)
fig = plt.figure(figsize=mpl_papersize('a5', 'landscape'))
labelpos = mpl_margins(fig, w=7., h=5., units=fontsize)
axes = fig.add_subplot(1, 1, 1)
labelpos(axes, 2., 1.5)

axes.set_xlabel('Distance [km]')
axes.set_ylabel('Time [s]')

axes.plot(phase_distances/km, phase_time, 'o', ms=3., color='black')

fig.savefig('cake_first_arrivals.pdf')

Calculate traveltimes in heterogeneous media

These examples demonstrate how to use the pyrocko.modelling.eikonal module to calculate first arrivals in heterogenous media.

eikonal_example1.py

import numpy as num
from matplotlib import pyplot as plt
from pyrocko.modelling import eikonal

km = 1000.
nx, ny = 1500, 500                # grid size
delta = 90*km / float(nx)         # grid spacing
source_x, source_y = 0.0, 15*km   # source position

# Indexing arrays
x = num.arange(nx) * delta - 2*km
y = num.arange(ny) * delta
x2 = x[num.newaxis, :]
y2 = y[:, num.newaxis]

# Define layers with different speeds, roughly representing a crustal model.
speeds = num.ones((ny, nx))
nlayer = ny // 5
speeds[0*nlayer:1*nlayer, :] = 2500.
speeds[1*nlayer:2*nlayer, :] = 3500.
speeds[2*nlayer:3*nlayer, :] = 5000.
speeds[3*nlayer:4*nlayer, :] = 6000.
speeds[4*nlayer:, :] = 8000.

# Seeding points have non-negative times. Here we simply set one grid node to
# zero. The solution to the eikonal equation is computed at all nodes where
# times < 0.
times = num.zeros((ny, nx)) - 1.0
times[int(round(source_y/delta)), int(round((source_x-x[0])//delta))] = 0.0

# Solve eikonal equation.
eikonal.eikonal_solver_fmm_cartesian(speeds, times, delta)

# Plot
fig = plt.figure(figsize=(9.0, 4.0))

axes = fig.add_subplot(1, 1, 1, aspect=1.0)
axes.contourf(x/km, y/km, times)
axes.invert_yaxis()
axes.contourf(x/km, y/km, speeds, alpha=0.1, cmap='gray')
axes.plot(source_x/km, source_y/km, '*', ms=20, color='white')
axes.set_xlabel('Distance [km]')
axes.set_ylabel('Depth [km]')
# fig.savefig('eikonal_example1.png')
plt.show()

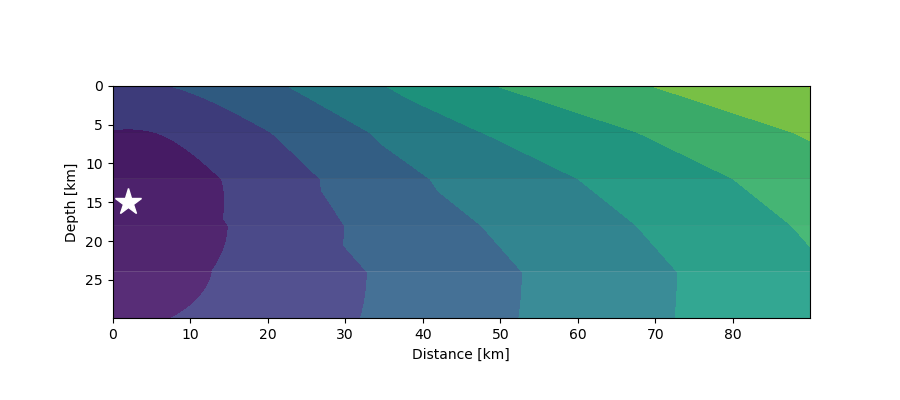
First arrivals (contours) from a seismic source (star) at 15 km depth in a 5-layer crustal model where velocities increase with depth.

eikonal_example2.py

import numpy as num
from matplotlib import pyplot as plt
from pyrocko.modelling import eikonal

km = 1000.
nx, ny = 1000, 500          # grid size
delta = 20*km / float(nx)   # drid spacing

# Indexing arrays
x = num.arange(nx) * delta - 10.0
y = num.arange(ny) * delta
x2 = x[num.newaxis, :]
y2 = y[:, num.newaxis]

# Define layers and circles with different speeds, roughly representing a case
# with two layers and intrusions.
speeds = num.ones((ny, nx))
r1 = num.sqrt((x2-0*km)**2 + (y2-2*km)**2)
r2 = num.sqrt((x2-12*km)**2 + (y2-0*km)**2)
nlayer = ny // 5
speeds[r1 < 4*km] = 2.0
speeds[r2 < 4*km] = 0.7
speeds[:3*nlayer, :] *= 0.5

# Seeding points have non-negative times. Here we
times = num.zeros((ny, nx)) - 1.0
times[-1, :] = (x-num.min(x)) * 0.1

# Solve eikonal equation.
eikonal.eikonal_solver_fmm_cartesian(speeds, times, delta)

# Plot
fig = plt.figure(figsize=(9.0, 4.0))

axes = fig.add_subplot(1, 1, 1, aspect=1.0)
axes.contourf(x/km, y/km, times)
axes.invert_yaxis()
axes.contourf(x/km, y/km, speeds, alpha=0.1, cmap='gray')
axes.set_xlabel('Distance [km]')
axes.set_ylabel('Depth [km]')
# fig.savefig('eikonal_example2.png')
plt.show()

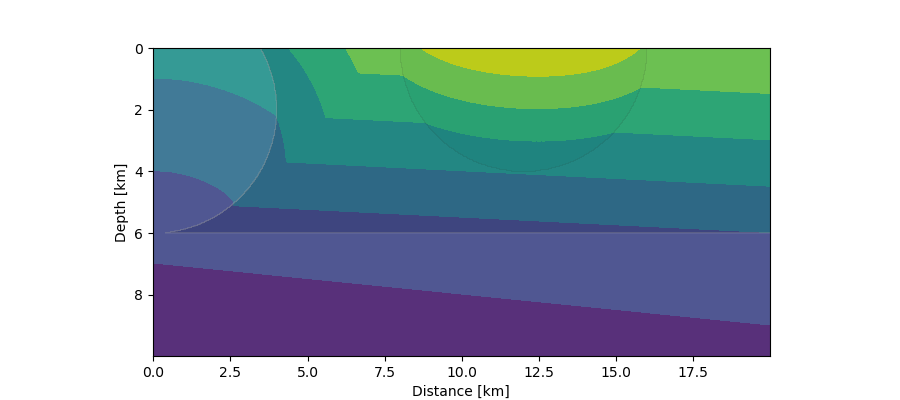
First arrivals (contours) from a distant seismic source in a 2-layer crustal model with intrusions. The planar wave front entering from below is simulated by a source at 10 km depth moving quickly from left to right with a given constant speed.

Traveltime table interpolation

This example demonstrates how to interpolate and query traveltime tables.

Classes covered in this example:

• pyrocko.spit.SPTree (interpolation of traveltime tables)

• pyrocko.gf.meta.TPDef (phase definitions)

• pyrocko.gf.meta.Timing (onset definition to query the travel time tables)

Download cake_raytracing.py

import numpy as num
import matplotlib.pyplot as plt
from pyrocko import spit, cake
from pyrocko.gf import meta


# Define a list of phases.
phase_defs = [meta.TPDef(id='stored:depth_p', definition='p'),
              meta.TPDef(id='stored:P', definition='P')]

# Load a velocity model. In this example use the default AK135.
mod = cake.load_model()

# Time and space tolerance thresholds defining the accuracy of the
# :py:class:`pyrocko.spit.SPTree`.
t_tolerance = 0.1                           # in seconds
x_tolerance = num.array((500., 500.))       # in meters

# Boundaries of the grid.
xmin = 0.
xmax = 20000
zmin = 0.
zmax = 11000
x_bounds = num.array(((xmin, xmax), (zmin, zmax)))

# In this example the receiver is located at the surface.
receiver_depth = 0.

interpolated_tts = {}

for phase_def in phase_defs:
    v_horizontal = phase_def.horizontal_velocities

    def evaluate(args):
        '''Calculate arrival using source and receiver location
        defined by *args*. To be evaluated by the SPTree instance.'''
        source_depth, x = args

        t = []

        # Calculate arrivals
        rays = mod.arrivals(
            phases=phase_def.phases,
            distances=[x*cake.m2d],
            zstart=source_depth,
            zstop=receiver_depth)

        for ray in rays:
            t.append(ray.t)

        for v in v_horizontal:
            t.append(x/(v*1000.))
        if t:
            return min(t)
        else:
            return None

    # Creat a :py:class:`pyrocko.spit.SPTree` interpolator.
    sptree = spit.SPTree(
        f=evaluate,
        ftol=t_tolerance,
        xbounds=x_bounds,
        xtols=x_tolerance)

    # Store the result in a dictionary which is later used to retrieve an
    # SPTree (value) for each phase_id (key).
    interpolated_tts[phase_def.id] = sptree

    # Dump the sptree for later reuse:
    sptree.dump(filename='sptree_%s.yaml' % phase_def.id.split(':')[1])

# Define a :py:class:`pyrocko.gf.meta.Timing` instance.
timing = meta.Timing('first(depth_p|P)')


# If only one interpolated onset is need at a time you can retrieve
# that value as follows:
# First argument has to be a function which takes a requested *phase_id*
# and returns the associated :py:class:`pyrocko.spit.SPTree` instance.
# Second argument is a tuple of distance and source depth.
z_want = 5000.
x_want = 2000.
one_onset = timing.evaluate(lambda x: interpolated_tts[x],
                            (z_want, x_want))
print('a single arrival: ', one_onset)


# But if you have many locations for which you would like to calculate the
# onset time the following is the preferred way as it is much faster
# on large coordinate arrays.
# x_want is now an array of 1000 distances
x_want = num.linspace(0, xmax, 1000)

# Coords is set up of distances-depth-pairs
coords = num.array((x_want, num.tile(z_want, x_want.shape))).T

# *interpolate_many* then interpolates onset times for each of these
# pairs.
tts = interpolated_tts['stored:depth_p'].interpolate_many(coords)

# Plot distance vs. onset time
plt.plot(x_want, tts, '.')
plt.xlabel('Distance [m]')
plt.ylabel('Travel Time [s]')
plt.show()