Kinematic/Dynamic source parameter modeling/inversion

Calculate subfault dislocations from tractions with Okada half-space equation

In this example we create a OkadaSource and compute the spatial quasi-static dislocation field caused by a traction field. The linear relation between traction and dislocation is calculated based on Okada (1992) [1].

Download okada_inversion_example.py

import numpy as num

from pyrocko.modelling import OkadaSource, invert_fault_dislocations_bem
from pyrocko.plot import dislocation as displt

km = 1e3

# Set source parameters
ref_north = 0*km
ref_east = 0*km
ref_depth = 50.*km

length_total = 50. * km
width_total = 15. * km

nlength = 20  # number of subpatches
nwidth = 16
npoints = nlength * nwidth

al1 = -length_total / 2.
al2 = length_total / 2.
aw1 = -width_total / 2.
aw2 = width_total / 2.

source = OkadaSource(
    lat=0., lon=0., north_shift=ref_north, east_shift=ref_east,
    depth=ref_depth,
    al1=al1, al2=al2, aw1=aw1, aw2=aw2, strike=45., dip=0.,
    slip=1., opening=0., poisson=0.25, shearmod=32.0e9)

# Discretize source and set receiver locations on source plane center points
source_discretized, _ = source.discretize(nlength, nwidth)

receiver_coords = num.array([
    src.source_patch()[:3] for src in source_discretized])

# Create stress drop (traction) array with spatial varying traction vectors
dstress = -1.5e6
stress_comp = 1

stress_field = num.zeros((npoints * 3, 1))

for il in range(nlength):
    for iw in range(nwidth):
        idx = (il * nwidth + iw) * 3
        if (il > nlength / 2. and il < nlength - 4) and \
                (iw > 2 and iw < nwidth - 4):
            stress_field[idx + stress_comp] = dstress
        elif (il > 2 and il <= nlength / 2.) and \
                (iw > 2 and iw < nwidth - 4):
            stress_field[idx + stress_comp] = dstress / 4.

# Invert for dislocation on source plane based on given stress field
disloc_est = invert_fault_dislocations_bem(
    stress_field, source_list=source_discretized, nthreads=0)

# Plot
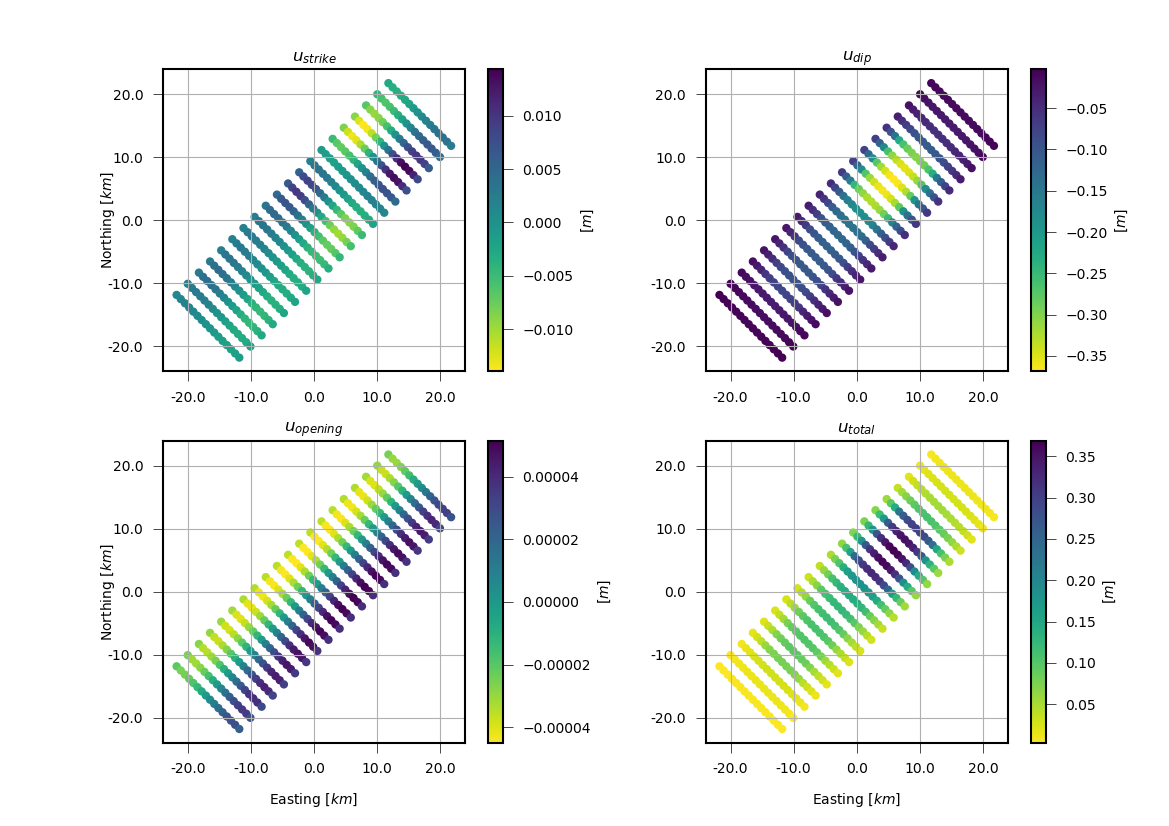
displt.plot(
    disloc_est.reshape(npoints, 3),
    receiver_coords,
    titles=['$u_{strike}$', '$u_{dip}$', '$u_{opening}$', '$u_{total}$'],
    cmap='viridis_r')

Footnotes

[1]	Okada, Y., Gravity and potential changes due to shear and tensile faults in a half-space. In: Journal of Geophysical Research 82.2, 1018–1040. doi:10.1029/92JB00178, 1992.